Blog2: Conditional Neural Processes

paper
cnp
Published

September 16, 2025

1 Research problem

Neural networks excel at function approximation but must be retrained from scratch for every new function. Bayesian methods such as Gaussian processes (GPs), by contrast, exploit prior knowledge to infer the shape of a previously unseen function at test time. Yet GPs are computationally expensive and crafting an appropriate prior is often difficult.

Conditional Neural Processes (CNPs) are a new class of neural models that combine the strengths of both approaches. Inspired by the flexibility of stochastic processes like GPs, CNPs retain the neural-network architecture and are trained by gradient descent. They yield accurate predictions after observing only a handful of training points, and scale to complex functions and large datasets. We demonstrate the performance and versatility of CNPs on a range of classic machine-learning tasks, including regression, classification and image completion.

2 Method

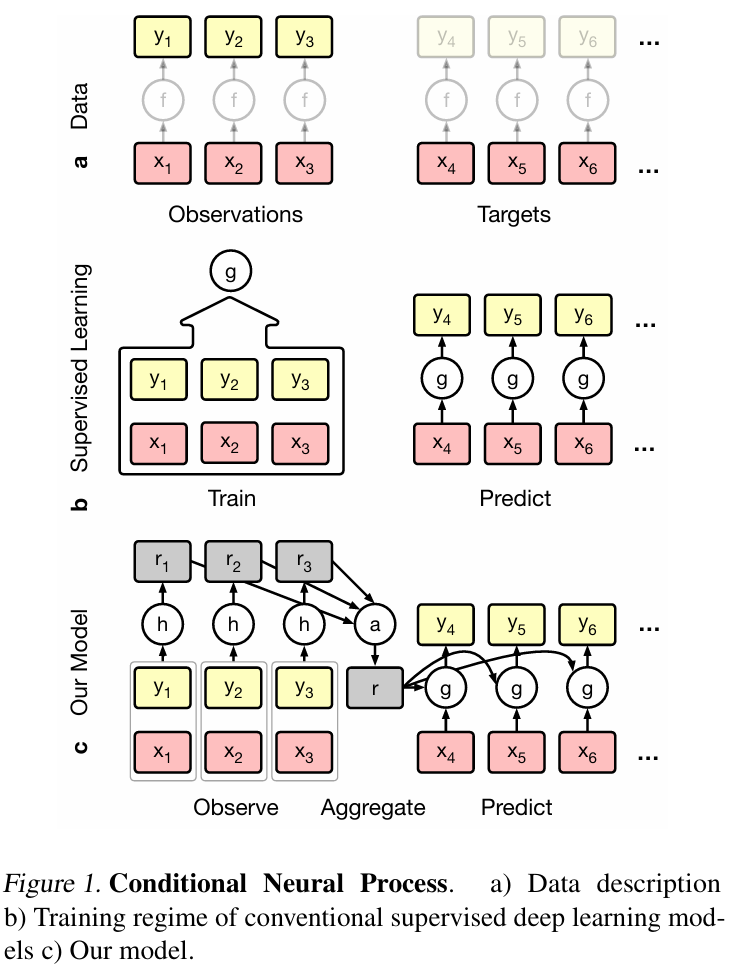
Figure 1: Conditional Neural Process

CNPs: observe → aggregate → predict 1. Embed every observation into a vector. 2. Combine these vectors with a symmetric aggregator (sum, mean, max, …) to produce a fixed-size embedding r. 3. Condition a function g on r to obtain predictions. (Symmetry ⇒ the aggregate is insensitive to the order of the inputs.)

Fixed dimension: the dimension of r is constant w.r.t. the number of observations n, so runtime does not grow exponentially with n.

Conditioning the function g: r is fed into another network that outputs the parameters (or full predictive distribution) of the target function g. For instance, g may be a network that emits the predictive distribution p(yⱼ | xⱼ, r) for a query location xⱼ.

Training is performed by sampling random datasets and performing gradient steps that maximize the conditional likelihood of a target subset given an observed subset. This procedure works whether the number of observed points n and target points m are equal or not.

Although CNPs share some traits with Bayesian methods, they do not perform Bayesian inference.

Similarities to Bayesian approaches

Both CNPs and Bayesian models (e.g., GPs) model conditional distributions over functions: after seeing data they return a full predictive distribution (mean and uncertainty) at new inputs. A CNP, like a GP, can emit p(yⱼ | xⱼ, {(xᵢ, yᵢ)}).

Differences—no Bayesian inference

  • Bayesian inference starts with an explicit prior p(f) and updates it to a posterior via Bayes’ rule: p(f | data) ∝ p(data | f) p(f).
  • CNPs never specify an explicit prior; instead, a neural network learns a direct mapping from observed data to a predictive distribution.
  • The “prior knowledge” in a CNP is encoded implicitly in the network weights learned from data, not in a mathematically prescribed prior such as a Gaussian process kernel.

Advantages of CNPs

  1. Data-driven prior: the model extracts prior information automatically from training data, eliminating manual kernel design.
  2. Efficient scaling: test-time complexity is O(n + m), enabling large-scale or real-time applications where GPs become prohibitive.

3 Experimental Results

3.1 Function Regression

1-D Regression a a kernel with fixed parameters

5 context points（left） & 50 context points（right）：GPs（red） & CNPs（blue）

b switching kernel task

3.2 Image Completion

Figure 2: Pixel-wise image regression on MNIST

As shown in the bottom row of Figure 3a, as we add more observations, the variance shifts from being almost uniformly spread over the digit positions to being localized around areas that are specific to the underlying digit, specifically its edges.

We test this by comparing the predictions of CNP when the observations are chosen according to uncertainty (i.e. the pixel with the highest variance at each step), versus random pixels (Figure 3b). This method is a very simple way of doing active exploration, but it already produces better prediction results than selecting the conditioning points at random.

Figure 3: Pixel-wise image completion on CelebA
Figure 4: Flexible image completion

3.3 Classification

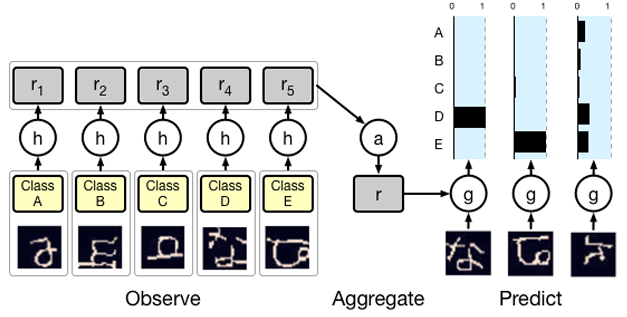
Figure 5: One-shot Omniglot classification

4 Conclusion

This paper has introduced Conditional Neural Processes, a model that is both flexible at test time and has the capacity to extract prior knowledge from training data.

This paper compared CNPs to Gaussian Processes on one hand, and deep learning methods on the other, and also discussed the relation to meta-learning and few-shot learning.

To summarize, this work can be seen as a step towards learning high-level abstractions, one of the grand challenges of contemporary machine learning. Functions learned by most conventional deep learning models are tied to a specific, constrained statistical context at any stage of training. A trained CNPis more general, in that it encapsulates the high-level statistics of a family of functions.

References

  • Conditional Neural Processes: Garnelo M, Rosenbaum D, Maddison CJ, Ramalho T, Saxton D, Shanahan M, Teh YW, Rezende DJ, Eslami SM. Conditional Neural Processes. In International Conference on Machine Learning 2018.
  • Neural Processes: Garnelo, M., Schwarz, J., Rosenbaum, D., Viola, F., Rezende, D.J., Eslami, S.M. and Teh, Y.W. Neural processes. ICML Workshop on Theoretical Foundations and Applications of Deep Generative Models 2018.
  • Attentive Neural Processes: Kim, H., Mnih, A., Schwarz, J., Garnelo, M., Eslami, A., Rosenbaum, D., Vinyals, O. and Teh, Y.W. Attentive Neural Processes. In International Conference on Learning Representations 2019.